XAU / PAXG-XAUT Pairs Stationarity Analysis

Find the notebook here.

This notebook will provide arbitrage indications for spot to asset-backed cryptocurrency pairs. In particular, the XAUt/USDt and PAXG/USDt pairs will be analyzed against spot gold - taking advantage of low volume pair trading. In addition, this notebook will aim to run statistical tests to identify stationarity and mean reversion.

Data Consolidation

Create a helper function to fetch the data from the pyth price oracle.

1
2
3
4
# fetch data from the 'pyth' price oracle.
import requests as req
def getBarsPyth(symbol, resolution, start, end):
  return req.get("https://benchmarks.pyth.network/v1/shims/tradingview/history?symbol={0}&resolution={1}&from={2}&to={3}".format(symbol, resolution, start, end)).json()

Fetch bars as objects from the helper function oracle for XAU/USD, XAUt/USD, PAXG/USD. Ensure that the start date is further than 2023-12-04 (listing date of XAUt) and is not a weekend (as XAU/USD does not trade on weekends).

1
2
3
4
5
6
7
8
9
# fetch bars as JSON objecobject
import time
import datetime as dt

interval = 60 # default = 60
start, end = dt.date(2024, 1, 4), dt.date.today() # default = 1/4/2024 -> today
XAU = getBarsPyth("Metal.XAU%2FUSD", interval, int(time.mktime(start.timetuple())), int(time.mktime(end.timetuple())))
XAUT = getBarsPyth("Crypto.XAUT%2FUSD", interval, int(time.mktime(start.timetuple())), int(time.mktime(end.timetuple())))
PAXG = getBarsPyth("Crypto.PAXG%2FUSD", interval, int(time.mktime(start.timetuple())), int(time.mktime(end.timetuple())))

Data Cleaning

With the dataset from pyth, place the datasets into a dictionary to then be merged into one DataFrame, using time (in UNIX) as an index.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# create timeseries as dict
import pandas as pd
import matplotlib.pyplot as plt

xau_pair = {'t': XAU['t'], 'c_xau': XAU['c']}
xaut_pair = {'t': XAUT['t'], 'c_xaut': XAUT['c']}
paxg_pair = {'t': PAXG['t'], 'c_paxg': PAXG['c']}

# merge data into dataframe (data)
df1, df2, df3 = pd.DataFrame(xau_pair), pd.DataFrame(xaut_pair), pd.DataFrame(paxg_pair)
df1.set_index('t', inplace=True)
df2.set_index('t', inplace=True)
df3.set_index('t', inplace=True)
merged = pd.concat([df1, df2, df3], axis=1, join='outer')
merged.sort_values(by='t', inplace=True)
merged = merged.reset_index()
merged['time'] = pd.to_datetime(merged['t'],unit='s')
merged = merged.set_index('t')
data = merged

Normalize XAU, XAUt, and PAXG by taking the percent difference of the closing price of each bar.

1
2
3
4
# adjust for price difference, normalize with pct change
data['pct_c_xau'] = (data['c_xau'] / data['c_xau'].iloc[0] - 1) * 100
data['pct_c_xaut'] = (data['c_xaut'] / data['c_xaut'].iloc[0] - 1) * 100
data['pct_c_paxg'] = (data['c_paxg'] / data['c_paxg'].iloc[0] - 1) * 100

Calculate the spread of each datapoint with respect to XAU (w/ a XAUt-PAXG spread).

1
2
3
4
5
6
7
8
9
# spread
data['pct_c_xau_interpolated'] = data['pct_c_xau'].interpolate(method='linear')
gold_i, paxg_i, xaut_i = data['pct_c_xau_interpolated'], data['pct_c_paxg'], data['pct_c_xaut']
aligned_goldGP, aligned_paxgGP = gold_i.align(paxg_i, join='outer')
aligned_goldGX, aligned_xautGX = gold_i.align(xaut_i, join='outer')
aligned_paxgPX, aligned_xautPX = paxg_i.align(xaut_i, join='outer')
data['spread_xaupaxg'] = aligned_goldGP - aligned_paxgGP
data['spread_xauxaut'] = aligned_goldGX - aligned_xautGX
data['spread_xautpaxg'] = aligned_xautPX - aligned_paxgPX

Data Analysis

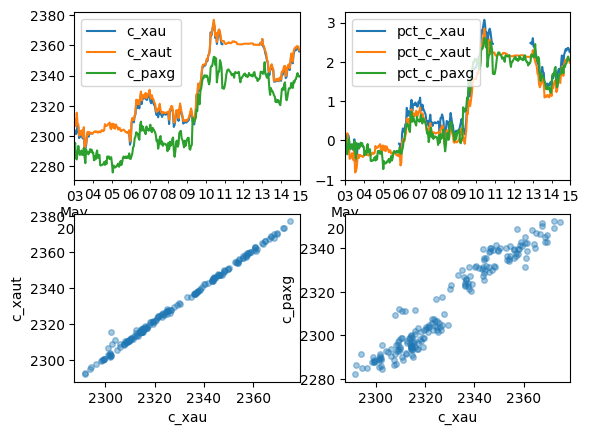
Let us plot the graph of PAXG, XAUt, and XAU - both raw and normalized; additionally plot the correlation of PAXG and XAUt with respect to XAU.

1
2
3
4
5
6
# graph of percent changes of gold, xaut, and paxg
fig, axes = plt.subplots(nrows=2, ncols=2)
data.loc[:,['c_xau', 'c_xaut', 'c_paxg', 'time']].plot(x = 'time', ax=axes[0,0])
data.loc[:,['pct_c_xau', 'pct_c_xaut', 'pct_c_paxg', 'time']].plot(x = 'time', ax=axes[0,1])
data.plot(kind='scatter', x='c_xau', y='c_xaut', s=16, alpha=0.4, ax=axes[1,0])
data.plot(kind='scatter', x='c_xau', y='c_paxg', s=16, alpha=0.4, ax=axes[1,1])
<AxesSubplot: xlabel='c_xau', ylabel='c_paxg'>
Image of the output 
1
data.loc[:,['pct_c_xau', 'pct_c_xaut', 'pct_c_paxg', 'time']].plot(x = 'time')
<AxesSubplot: xlabel='time'>
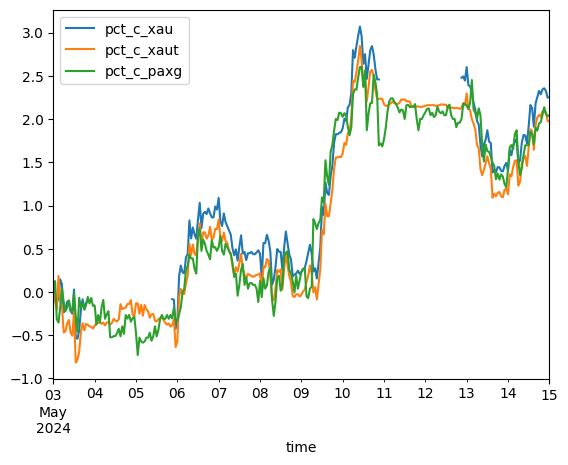
Image of the output

Analytically, we can show that XAU, XAUt, and PAXG all exhibit strong correlation. Since these datasets are meant to be directly proportional to each other, any variation we exhibit in this dataset is a theoretical risk-free profit. However, before we put these claims into practice, let us perform statistical tests to prove direct proportionality, stationarity, and mean reversion.

1
print(data.loc[:,['c_xau', 'c_xaut', 'c_paxg']].corr())

         c_xau        c_xaut       c_paxg

c_xau    1.000000     0.998364     0.964174

c_xaut   0.998364     1.000000     0.971587

c_paxg   0.964174     0.971587     1.000000

As this DataFrame is from January to Mid-May, on the assumption that this data isn't mean reverting [1], the expected loss for an unleveraged portfolio would be the spread between XAUt and PAXG. However, we see a strong positive correlation. To take advantage of spread trading, let us create three datasets - the spread between XAUt, PAXG w/ respect to XAU, and a XAUt-PAXG spread.

[1] A mean reverting series is a group of data that retains 'memory' - as a series deviate from a given mean, it tends to traverse back to the mean (hence 'reverting').

1
2
3
graph = data.copy()
graph['root'] = aligned_goldGP - aligned_goldGP # this is such a bad way to initialize all zero values.
graph.loc[:,['spread_xaupaxg', 'spread_xauxaut', 'spread_xautpaxg', 'root', 'time']].plot(x = 'time')
<AxesSubplot: xlabel='time'>
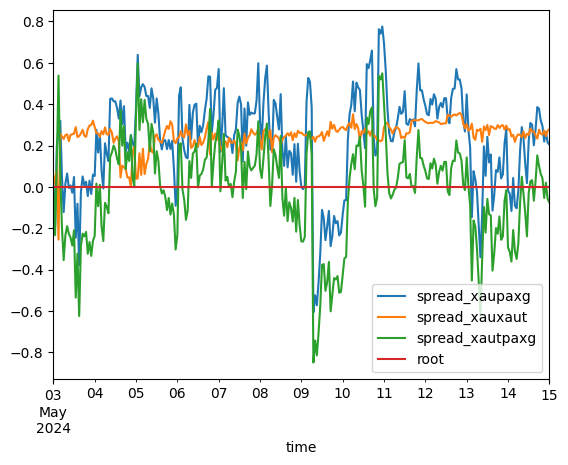
Image of the output

In a completely efficient market, we should expect absolutely no deviation in price - however that doesn't exist (I hate economists). To create a profit in this situation, one would short the base currency and long the trading currency (or vice versa, depending on the direction of the spread). To prove that this is truly risk-free, we must demonstrate that the PAXG, XAUT pair spreads exhibit mean reversion. A continuous mean-reverting time series can be represented by an Ornstein-Uhlenbeck stochastic differential equation:

\(dx_t = \theta (\mu - x_t) dt + \sigma dW_t\)

Where \(\theta\) is the rate of reversion to the mean, \(\mu\) is the mean value of the process, \(\sigma\) is the variance of the process, and \(W_t\) is a Wiener Process or a Brownian Motion. In a discrete setting, the equation states that the change of the price series in the next time period is proportional to the difference between the mean price and the current price, with the addition of Gaussian noise. This motivates the Augmented Dickey-Fuller Test, which we will describe below.

Augmented Dickey-Fuller Test

A unit root is a stochastic trend in a given series. The point of an Augmented Dickey-Fuller Test is to determine whether or not a unit root exists; if it does not exist, the series is not trending. As a result, a higher score in the Dickey-Fuller test indicates that there's a more prominent trend, and vice versa.

1
2
3
4
5
6
7
8
import statsmodels.tsa.stattools as ts
adf_xauxaut = ts.adfuller(data['spread_xauxaut'], 1) # perform adf on xau-xaut
adf_xaupaxg = ts.adfuller(data['spread_xaupaxg'], 1) # perform adf on xau-paxg
adf_xautpaxg = ts.adfuller(data['spread_xautpaxg'], 1) # perform adf on xaut-paxg
print("adfuller for XAU-XAUT: {0}".format(adf_xauxaut))
print("adfuller for XAU-PAXG: {0}".format(adf_xaupaxg))
print("adfuller for XAUT-PAXG: {0}".format(adf_xautpaxg))
print(type(adf_xaupaxg))
adfuller for XAU-XAUT: (-5.424463068477814, 3.0086787067634902e-06, 1, 287, {'1%': -3.453342167806272, '5%': -2.871663828287282, '10%': -2.572164381381345}, -963.8929704620568)
adfuller for XAU-PAXG: (-5.735268089050287, 6.460192127149706e-07, 0, 288, {'1%': -3.453261605529366, '5%': -2.87162848654246, '10%': -2.5721455328896603}, -304.917811118788)
adfuller for XAUT-PAXG: (-5.729545258695016, 6.649327955430402e-07, 0, 288, {'1%': -3.453261605529366, '5%': -2.87162848654246, '10%': -2.5721455328896603}, -277.07578574419176)
<class 'tuple'>

The ts.adfuller() API calls for returning a tuple with the following attributes:

Value Description
adf : float Test statistic
pvalue: float MacKinnon’s approximate p-value based on MacKinnon (1994, 2010)
usedlag: int Number of lags used
nobs: int Number of observations used for the ADF regression and calculation of the critical values
critical values: dict Critical values for the test statistic at the 1%, 5%, and 10% levels. Based on MacKinnon (2010)
icbest: float The maximized information criterion if autolag is not None.

As noted in the output [ref], all of our series have a \(p\)-value lower than \(0.01\), which is promising (we can now reject the null hypothesis of \(\gamma = 1\)). Let us reverify our observation by finding the Hurst Exponent.

Hurst Exponent

The Hurst exponent (HE) aims to provide us a scalar value that helps us identify the 'memory' of a series (i.e. mean reversion). A series with \(HE > 0.5\) is said to be trending, \(HE = 0.5\) is said to be GBM (random walk), and \(HE < 0.5\) is categorized as mean reverting.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# create hurst exponent function
import numpy as np
from numpy import cumsum, log, polyfit, sqrt, std, subtract

# input is numpy array
def hurst(ts):
    lags = range(2, 100) # create the range of lagging values
    tau = [sqrt(std(subtract(ts[lag:], ts[:-lag]))) for lag in lags] # variance
    m = polyfit(log(lags), log(tau), 1) # polynomial fit
    return m[0] * 2 # return exponent

print("hurst(XAU-XAUT): {0}".format(hurst(data['spread_xauxaut'].values)))
print("hurst(XAU-PAXG): {0}".format(hurst(data['spread_xaupaxg'].values)))
print("hurst(XAUT-PAXG): {0}".format(hurst(data['spread_xautpaxg'].values)))
hurst(XAU-XAUT): 0.02211187342168529
hurst(XAU-PAXG): 0.1254107697763245
hurst(XAUT-PAXG): 0.11409796976657859

Nice.